MACHINES À COURANT CONTINU

Chapitre 1 :

Machines à courant continu :

Les dynamos à courant continu ont été les premiers convertisseurs électromécaniques utilisés. Leur usage est en régression très nette en particulier en tant que générateurs de courant. On utilise de préférence des redresseurs à semi-conducteurs alimentés par des alternateurs. Les moteurs à courant continu restent très utilisés dans le domaine de l’automobile (ventilateurs, lève-vitre, etc.) ainsi qu’en tant que « moteur universel » dans l’électroménager et l’outillage. Dans le domaine des puissance supérieure au mégawatt, les sous-marins seront les seuls utilisateurs de machines à courant continu afin d’assurer leur propulsion. En effet, pour éviter de « rayonner » du 50 ou du 60 Hertz qui les rendrait facilement détectables, les sous-marins utilisent des circuits de distribution de l’énergie électrique à tensions continues. La fabrication de machine à courant continu de puissance supérieure à 10MW se heurte à une frontière technologique infranchissable. En effet, les problèmes d’injection de courant par les contacts balais - collecteur posent des problèmes insolubles au dessus de ce seuil de puissance.

 1.1 Symboles :

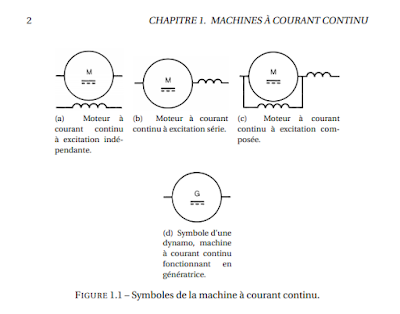
Voici les différents symboles employés pour représenter la machine à courant continu, selon qu’elle fonctionne en génératrice (dynamo) ou en moteur et selon le type d’excitation employée.

1.2 Constitution d’une machine à courant continu :

Une machine à courant continu comprend quatre parties principales : — l’inducteur ; — l’induit ; — le collecteur ; — les balais également appelés charbons.

1.2.1 L’inducteur

Le bobinage inducteur, traversé par le courant inducteur Ie , produit le flux magnétique dans la machine. Il est constitué d’un électro-aimant qui engendre la force magnétomotrice (F.M.M.) nécessaire à la production du flux. Dans les machines bipolaires (à deux pôles), deux bobines excitatrices sont portées par

1.2. CONSTITUTION D’UNE MACHINE À COURANT CONTINU :

deux pièces polaires montées à l’intérieur d’une culasse. La culasse est généralement en fonte d’acier, tandis que les pièces polaires sont formées de tôles d’acier doux, voir figure 1.3 page suivante page suivante et 1.4 page 5 page 5. Les bobines excitatrices sont alimentées en courant continu, et le courant qui les traverse porte le nom de courant d’excitation (Ie ). Ces bobines sont composées de plusieurs centaines de spires et sont traversées par un courant relativement faible. Dans certaines machines, les bobines et les pièces polaires sont remplacées par des aimants permanents. Le champ magnétique créé par la F.M.M. des bobines traverse les pièces polaires, la culasse, l’induit et l’entrefer. L’entrefer est l’espace d’air séparant la surface de l’induit de celle des pièces polaires : il est de l’ordre de 1,5 à 5 mm pour les machines de faible et moyenne puissance. Comme l’induit et l’inducteur sont construits avec des matériaux de faible réluctance, la majeure partie de la F.M.M. sert à « pousser » le flux à travers l’entrefer. Celui-ci doit donc être aussi peu long que possible. Le nombre de pôles que porte l’inducteur d’une machine à courant continu dépend surtout de la grosseur de la machine. Plus une machine est puissante et plus sa vitesse est basse, plus grand sera le nombre de pôles. Les bobines excitatrices d’un inducteur multipolaire sont connectés de façon à ce que les pôles adjacents soient de polarités magnétiques opposées.

 1.2.2 L’induit :

L’induit est composé d’un ensemble de bobines identiques réparties uniformément autour d’un noyau cylindrique. Il est monté sur un arbre et tourne entre les pôles de l’inducteur. L’induit constitue un ensemble de conducteurs qui coupent les lignes de champ magnétique. Les bobines sont disposées de telle façon que leurs deux côtés coupent respectivement le flux provenant d’un pôle nord et d’un pôle sud de l’inducteur. Le noyau est formé d’un assemblage de tôles en fer doux. Ces tôles sont isolées électriquement les unes des autres et portent des encoches destinées à recevoir les bobines, voir figure 1.6 page 7 page 7. Les conducteurs de l’induit sont parcourus par le courant absorbé ou débité par la machine. Ils sont isolés du noyau par des couches de feuilles isolantes, voir figure 1.8 page 8. Pour résister aux forces centrifuges, ils sont maintenus

1.2. CONSTITUTION D’UNE MACHINE À COURANT CONTINU :

CHAPITRE 1. MACHINES À COURANT CONTINU ::

solidement en place dans les encoches au moyen de cales en fibre de verre. Si le courant est inférieur à une cinquantaine d’ampères, on emploie des conducteurs ronds. Au delà de 50 A, les conducteurs sont rectangulaires, ce qui permet une meilleure utilisation du volume de l’encoche.

1.2.3 Collecteurs et balais :

Le collecteur est un ensemble cylindrique de lames de cuivre isolées les unes des autres par des feuilles de mica. Le collecteur est monté sur l’arbre de la machine, mais isolé de celui-ci. Les deux fils sortant de chaque bobine de l’induit sont successivement et symétriquement soudés aux lames du collecteur. Dans une machine bipolaire, deux balais fixes et diamétralement opposés appuient sur le collecteur. Ainsi, ils assurent le contact électrique entre l’induit

et le circuit extérieur. La construction du collecteur relève de la mécanique de précision, voir figure 1.12 page suivante page suivante. Les machines multipolaires ont autant de balais que de pôles. Les balais permettent l’injection ou la collecte du courant sur le collecteur. Lors de la construction des premières machines à courant continu, les balais étaient constitués de fils de cuivre disposés comme la paille de riz ou les branches sur les balais pour nettoyer, d’où le nom de balais (voir figure 1.13 page 13). Les balais (aussi appelés « charbon ») sont en carbone (on choisit souvent du graphite). D’une part, ce matériaux possède une bonne conductivité d’autre part, le frottement du couple cuivre/carbone est faible et ainsi, le collecteur ne s’use pas prématurément. La pression des balais sur le collecteur peut être réglée par des ressorts ajustables. Pour les intensités très importantes, on utilise plusieurs balais connectés en parallèle, voir figure 1.14 page 14.

1.3 Équation générale :

1.3.1 Force électromotrice à vide : Nous avons vu au chapitre précédent qu’il était possible d’obtenir une f.é.m. continue en mettant en série les conducteurs de l’induit et en recueillant cette f.é.m. par deux balais fixes par rapport à l’inducteur et placés sur la ligne neutre. La « ligne neutre » est l’axe de symétrie d’une machine bipolaire, perpendiculaire à une ligne joignant les pôles.

1.3.1.1 f.é.m. réellement obtenue :

Prenons par exemple un induit comportant 8 conducteurs comme le montre la figure 1.15 (n = 8) et étudions la tension obtenue. Le nombre de conducteurs étant fini, la tension obtenue entre B et B’ ne sera pas rigoureusement constante. Les schémas de la figure 1.15 représentent le circuit de l’induit et les f.é.m. des conducteurs. Les f.é.m. 1-1’, 2-2’, ... ont respectivement même module. Á l’instant t, les conducteurs 1 et 1’, par exemple, sont en contact avec les balais. Pendant le passage des conducteurs sous les balais, la tension varie : elle est maximale quand 1 et 1’ sont sur la ligne neutre. Quand 1 et 1’ quittent les

balais, 4’ et 4 les remplacent à t +∆t ; les noms des conducteurs changent mais la répartition des f.é.m. reste identique. On obtient une tension ondulée comme le montre la figure 1.16. L’ondulation est d’autant plus faible que le nombre n de conducteurs est élevé (∆t petit). La tension maximale est sensiblement égale à nNΦ et on peut en général négliger l’ondulation qui ne représente que quelques pour cents de la tension

1.3.1.2 Bobinage de l’induit ; collecteur :

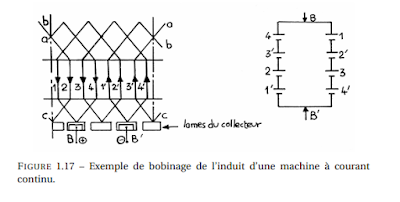
Il existe de nombreux procédés de mise en série des conducteurs de l’induit. D’autre part, les balais ne frotteront pas directement sur les conducteurs mais sur des lames de cuivre reliées aux conducteurs et constituant le collecteur. EXEMPLE DE RÉALISATION : Les connexions sont effectuées à l’avant et à l’arrière de l’induit et, à la figure 1.17 page suivante on représente la surface latérale du rotor. Les flèches indiquent le sens des f.é.m. à l’instant t. On réalise en fait la mise en série représentée sur la figure 1.17 page ci-contre, mais comme 1 = 1 0 , 2 = 2 0 , 3 = 3 0 , 4 = 4 0 la tension entre les balais B et B’ est la même que précédemment. REMARQUE : Bien que reliés aux conducteurs situés le plus près de la ligne neutre, les balais, du fait du bobinage et du collecteur, sont placés dans l’axe des pôles inducteurs comme l’indique la figure 1.18 page suivante.

1.3.1.3 Formule générale de la force électromotrice :

On a donc : E = nNΦ

1.3. ÉQUATION GÉNÉRALE :

Si l’inducteur comporte 2p pôles, il revient au même de considérer une machine bipolaire avec un induit qui tourne p fois plus vite que dans la machine à 2p pôles, soit N ⇒ pN Nous avons vu d’autre part qu’entre les balais, 2 trajets ou « voies d’enroulement » existent pour le courant. Certains enroulement d’induit permettent de répartir les n conducteurs en 2a voies soit : n ⇒ n a D’où la formule générale : E = p a nNΦ(Ie ) où p, a, n, sont des paramètres fixés par construction, et on écrira plus simplement : 

                                E = kNΦ(Ie )

La relation entre le flux et le courant d’excitation Ie n’étant pas, en général, mesurable directement, on utilise la courbe expérimentale donnant, à vitesse constante N0, la f.é.m. E en fonction du courant d’excitation Ie : c’est la caractéristique à vide de la machine, obtenue par l’essai à vide. Dans cet essai, la machine est entraînée à vitesse constante N0 par un moteur auxiliaire ; on fait varier Ie et on mesure E. Pour les faibles valeurs de Ie , le fonctionnement est à peu près linéaire et on peut poser :

                                      E = k 0N0Ie

Lorsque Ie augmente, le circuit magnétique se sature et la f.é.m. augmente moins fortement. Enfin, l’hystérésis introduit un dédoublement des courbes, fonction des cycles effectués. Il subsiste généralement une f.é.m. rémanente Er en l’absence du courant d’excitation Ie .

1.3.2 Étude en charge :

1.3.2.1 Couple électromagnétique    :    Lorsqu’un courant I circule dans l’induit, il apparaît un couple électromagnétique Ce créé par les forces de Laplace qui s’exercent sur les conducteurs de l’induit.

Ce = ΣFe ×r avec r rayon de l’induit. Ce couple ne dépend que de I et de l’induction B ou du flux Φ. On pourrait en faire le calcul direct en utilisant l’expression précédente ; il est plus simple d’effectuer un bilan de puissance. En vertu du théorème de Thévenin, le circuit d’induit, entre les deux balais, présente une f.é.m. E et une résistance R égale à la résistance mesurée aux bornes lorsque E est nulle, c’est à dire à l’arrêt de la machine. On considérera uniquement les régimes permanents où tensions d’alimentation et courants absorbés sont constants, ainsi on ne prendra pas en compte l’inductance de l’induit. Le schéma équivalent est celui de la figure 1.21 page suivante. Supposons que le courant I est absorbé par l’induit sous la tensionU (convention récepteur). La puissance P absorbée par l’induit peut s’écrire :                P =U I = (E +R I)I = E I +R I 2

R I 2 représente l’échauffement par pertes Joule de l’induit et des balais. E I représente la puissance qui disparaît de la forme électrique pour réapparaître sous la forme mécanique. C’est la puissance électromagnétique Pe qui présente deux écritures :

FIGURE 1.21 – Schéma équivalent de Thévenin d’une machine à courant continu.

P = E I = CeΩ = Ce2πN Soit : Ce = E I 2πN ou en remplaçant E :

                                                                          

                                                                   Ce = k 2π IΦ(Ie )

Le couple ne dépend que des courants. Son signe dépend du sens du courant. Ici, la convention choisie correspond à la fourniture de puissance mécanique (Ce et N de même sens) c’est à dire moteur.

1.3.2.2 Réaction d’induit :

La circulation des courants dans l’induit s’accompagne de phénomènes parasites : — Résistance de l’induit et des contacts balais/collecteur : Cette résistance R, rencontrée au paragraphe précédent, est la résistance équivalente aux 2a voies d’enroulement mises en parallèle, en série avec la résistance des contacts balais/collecteur. Le phénomène est cependant plus complexe car le contact balais/collecteur se présente comme une résistance non linéaire (fonction du courant I). La chute de tension dans les contacts balais/collecteur restant faible, on négligera ce phénomène et on mesurera R pour des courants proches du courant nominal. — Réaction magnétique de l’induit : Le passage du courant I produit une force magnétomotrice perpendiculaire à l’axe des pôles qui modifie la topographie des lignes d’induction. En fonctionnement moteur, on a les sens de courants indiqués sur la figure 1.22 page suivante. L’induit constitue une bobine qui crée le flux de réaction d’induit Φr . La ligne neutre est décalée en sens inverse de la rotation et les balais ne recueillent plus la f.é.m. maximale : la réaction magnétique de l’induit entraîne donc une réduction de f.é.m. en charge. Pour rendre cet effet négligeable devant la chute ohmique, on utilise des pôles auxiliaires, excités par le courant de l’induit et qui créent une force magnétomotrice opposée à celle de l’induit comme le montre la figure 1.23 page suivante.

Commutation : Lorsque le balai passe d’une lame du collecteur à la suivante, il y a court-circuit momentané d’une section du bobinage induit et, pendant ce temps, le courant doit changer de sens dans les conducteurs en commutation ; l’inductance de la section s’oppose à cette inversion et conduit à l’apparition d’étincelles (arcs) de commutation. Les pôles auxiliaires favorisent la commutation.

1.4 Moteur à courant continu :          L’utilisateur d’un moteur s’intéresse en premier lieu à la caractéristique mécanique Ce = f (N) qui donne le couple produit en fonction de la vitesse. Il faut par ailleurs connaître le courant absorbé en fonction du couple demandé : c’est la caractéristique électromécanique Ce = f (I). On utilise aussi la caractéristique de vitesse N = f (I). Ces courbes sont généralement tracées avec pour paramètres la tension d’alimentation U ; les propriétés obtenues dépendent du mode d’excitation.

1.4.1 Démarrage d’un moteur :

Si, lorsque la vitesse du moteur est nulle, on applique une tension U aux bornes de l’induit, le courant circulant dans l’induit est alors : ID = U R puisque la f.é.m. est nulle (N = 0). Ce courant est très supérieur au courant nominal (10 à 100 fois), ce qui entraînerait : — un échauffement instantané de l’induit très élevé ; — une chute de tension inadmissible sur le réseau d’alimentation ; — un couple de démarrage lui aussi très supérieur au couple nominal et risquant de rompre l’accouplement. Aussi faut-il limiter le courant d’induit en plaçant, lors du démarrage, une résistance RD en série avec l’induit. Ce rhéostat de démarrage est court-circuité progressivement tandis que le moteur prend sa vitesse et que la f.é.m. augmente. ID = U R +RD On calcule RD afin que ID soit de 1 à 2 fois le courant nominal In. Pour que le démarrage soit rapide, il faut que le couple soit élevé donc que le flux soit alors maximum (Ie maximum). NOTA : On peut aussi limiter le courant en utilisant un limiteur électronique ; d’autre part, si le démarrage s’opère sous tension variable U, il suffira de faire croître U progressivement.

1.4.2 Moteur à excitation séparée (ou dérivée) :

On alimente en parallèle sous la tension continue U l’induit et l’inducteur comme le montre la figure 1.26. On étudiera les caractéristiques pour U = c te et Ie = c te. On charge le moteur en lui opposant un couple résistant et on étudie : Ce = f (I) ; N = f (I) ; Ce = f (N). COUPLE : Ce = k 2π IΦ(Ie ) = E(N0,Ie ) 2πN0 I

Pour chaque valeur de Ie , le couple est donc proportionnel au courant d’induit I. La formule ci-dessus permet, en utilisant la caractéristique à vide, de calculer la pente de cette droite. On remarque que le courant ne dépend que du couple. On peut remarquer qu’au démarrage : CD = k 2π IDΦ(Ie ) = E(N0,Ie ) 2πN0 ID VITESSE : La loi d’Ohm appliquée à l’induit s’écrit :

U = E +R I ou E =U −R I = kNΦ(Ie )

                                                                          

                                                                             N = U −R I kΦ(Ie )

ou, en reprenant la caractéristique à vide (formule quantitative) :

N N0 = E(N,Ie ) E(N0,Ie ) = U −R I E(N0,Ie )

Pour chaque valeur de Ie , le dénominateur est constant et N est donc fonction linéaire du courant I. Pour un courant nul (donc pour un couple nul), on obtient la vitesse à vide NV :

NV = N0 U E(N0,Ie )

En charge, la vitesse diminue légèrement, car, en pratique, on aura R I 6 R In ¿U. CARACTÉRISTIQUE MÉCANIQUE : On élimine le courant entre les expressions précédentes :

N = U kΦ(Ie ) − · R kΦ(Ie ) 2π kΦ(Ie ) ¸ Ce

Pour chaque valeur de Ie , la vitesse est une fonction linéaire du couple. Le fonctionnement moteur correspond à Ce et N de même sens. Lorsque Ce et I sont ici négatifs, il s’agit d’un freinage : la charge est alors motrice (ou entraînante) et le courant est envoyé vers le réseau. REMARQUES : — Si Ie augmente le flux augmente, la vitesse diminue. — Si Ie diminue au contraire, la vitesse augmente et si Ie tend vers zéro, la vitesse à vide tend vers l’infini : en l’absence d’excitation, le moteur s’emballe. Il ne faut donc jamais couper ce circuit. — Si la tension U augmente, la vitesse augmente proportionnellement.

1.4.3 Moteur à excitation série :

On utilise un moteur dont l’inducteur, réalisé en conducteur de forte section, peut-être mis en série avec l’induit (voir figure 1.28). On impose donc : I = Ie , ce qui modifie les propriétés du moteur. On étudiera les caractéristiques sous tension constante U. COUPLE :

Ce = k 2π IΦ(I) = E(N0,I) 2πN0 I

Pour les faibles valeurs de I, le flux est proportionnel à I et le couple est donc proportionnel au carré du courant d’induit ; en posant : E(N0,I) = k 0N0I,

on a en effet :

Ce = k 0 2π I 2

Lorsque I augmente, le circuit magnétique se sature, le flux croît moins fortement, de même que le couple. On trace la courbe point par point à partir des valeurs de la caractéristique à vide. On remarque ici encore que le courant d’induit est lié au couple. NOTA : Au démarrage : CeD = k 2π IDΦ(ID) = E(N0,ID ) 2πN0 ID Ce couple pourra donc être très élevé (ID > In). VITESSE : En notant Rs la résistance de l’inducteur série, la loi d’Ohm s’écrit :

E =U −(R +Rs)I = kNΦ(I) 

D’où : N = U−(R+Rs)I kΦ(I) ou, en reprenant la caractéristique à vide :

N N0 = E(N,I) E(N0,I) = U −(R +Rs)I E(N0,I)

Le dénominateur dépend fortement de I. En particulier pour les faibles valeurs de I, on peut poser :

E(N0,I) = k 0N0I

Soit :

N N0 = U −(R +Rs)I k 0N0I

Lorsque I tend vers zéro (fonctionnement à vide, Ce = 0) la vitesse tend vers l’infini : il y a emballement à vide. La courbe présente une allure hyperbolique et la vitesse est nulle pour un courant I = U R+Rs In, voir figure 1.29 page ci-contre. CARACTÉRISTIQUES MÉCANIQUES : Il faut éliminer I entre les expressions du couple et de la vitesse. Comme I intervient dans la f.é.m., il faut procéder point par point. Pour un couple nul, on trouve un courant nul et une vitesse infinie ;

l’allure de la courbe est hyperbolique. On n’envisage pasCe < 0 car il faut passer par N = ∞ pour atteindre ce domaine, voir figure 1.29. REMARQUES : 1. Si U augmente, le couple reste inchangé et la vitesse augmente proportionnellement à U. 2. Le moteur série peut être utilisé en courant alternatif car le couple est proportionnel au carré du courant, donc toujours de même signe. Le circuit magnétique doit être entièrement feuilleté pour réduire les pertes fer et le moteur utilisable en alternatif ou en continu porte le nom de moteur universel. Il est très utilisé pour les petites puissances car sa vitesse n’est pas liée à la fréquence du réseau.

1.4.4 Moteur à excitation composée :

Le moteur à excitation séparée ne s’emballe pas à vide et répercute sur le courant I tout accroissement de couple ; le moteur série s’emballe, mais réduit les appels de courant lors d’une augmentation de couple I v p C. Pour concilier les avantages, on utilise un moteur comportant sur les pôles deux inducteurs : — l’un dérivé, comportant Ne spires, branché en parallèle et parcouru par le courant Ie ; — l’autre série, comportant Ns spires, branché en série, parcouru par le courant I.

La force magnétomotrice est donc Ne Ie ± NsI, le signe dépendant des sens relatifs des enroulements : ⊕ montage additif ª montage soustractif. Il est commode de considérer un courant fictif I 0 e , qui, circulant seul dans l’inducteur dérivé produirait le même flux :

Ne I 0 e = Ne Ie ± NsI

soit :

 0 e = Ie ±αI

ou α est le rapport d’équivalence. Ce courant équivalent permet de toujours se ramener à la caractéristique à vide tracée en excitation séparée en fonction de Ie seul. On obtient le schéma équivalent de la figure 1.31 page ci-contre, dans laquelle on inclut dans R 0 la résistance Rs de l’inducteur série :

R 0 = Rs +R

On étudie les courbes pour U = c ste ; Ie = c ste. COUPLE :

Ce = k 2π IΦ(I 0 e ) = E(N0,I 0 e 2πN0 I

On trace point par point la courbe de couple : si le montage est additif, I 0 e augmente avec I et le couple est supérieur à celui obtenu en excitation séparée seule. VITESSE :

E =U −R 0 I = kNΦ(I 0 e )

et

N N0 = U −R 0 I E(N0,I 0 e

A vide, le couple et I sont nuls : I 0 e = Ie . On retrouve la même vitesse Nv qu’en excitation séparée (l’enroulement série est sans effet). Si le montage est additif, le flux étant accru par le courant I, la vitesse est plus faible qu’en excitation séparée. Si le montage est soustractif, la réduction de flux due au courant entraîne un accroissement de la vitesse en charge pouvant conduire à l’emballement : le montage soustractif est à proscrire (N → ∞ si I 0 e → 0). CARACTÉRISTIQUES MÉCANIQUES : On l’obtient en éliminant graphiquement I entre les courbes précédentes, voir figure 1.32 page suivante. Comme, en pratique, α est faible, il est inutile de comparer ces courbes à celles du même moteur en excitation séparée seule. on voit que la courbe